hi guys its rajiv

Example:

In how many ways can 6 people be seated in a row of 6 chairs?

Solution:

We can use the permutation formula P(6, 6) which is 6 things taken 6 at a time.

P(6, 6) = 6 × 5 × 4 × 3 × 2 × 1

Six people can be seated in 720 ways.

Example:

In how many ways can seven different books be arranged on the shelf?

Solution:

We can use the permutation formula P(7, 7) which is 6 things taken 6 at a time.

P(7, 7) = 7 × 6 × 5 × 4 × 3 × 2 × 1

The books can be arranged in 5,040 ways.

We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.

We know the factorial is: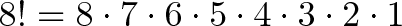

Unfortunately, that does too much! We only want 8 * 7 * 6. How can we “stop” the factorial at 5?

This is where permutations get cool: notice how we want to get rid of 5*4*3*2*1. What’s another name for this? 5 factorial!

So, if we do 8!/5! we get:

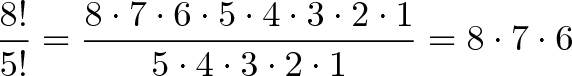
The total no. of permutations of n objects taken r at a time, P(n,r) is given by the expression.

P (n,r) = nPr = n!/(n-r)!

Problem:

Find the no. of permutations of the four integers 1,2,3,4 taken two at a time.

Solution:

n = 4, r = 2

4P2 = n!/(n-r)! = 4!/(4-2)! = 4!/2! = 4.3.2.1 / 2.1 = 12

Example 3. Express ¹⁰P₄ in terms of factorials.

Solution.

10P4

=

10! 6!

The upper factorial is the upper index, and the lower factorial is the difference of the indices. When the 6!'s cancel, the numerator becomes 10· 9· 8· 7.

This is the number of permutations of 10 different things taken 4 at a time.

Example 4. Calculate ⁿP_n.

Solution. nPn

=

n! (n − n)!

=

n! 0!

=

n! 1

= n!

ⁿP_n is the number of permutations of n different things taken n at a time -- it is the total number of permutations of n things: n!. Thedefinition 0! = 1 makes line (1) above valid for all values of k: k = 0, 1, 2, . . . , n.

Formula:
	Note: , where nPr is the formula for permutations of nobjects taken r at a time. Example: How many different committees of 4 students can be chosen from a group of 15? Answer: There are possible combinations of 4 students from a set of 15. There are 1365 different committees.