Good evening everyone! It's Sheena :D

What we learned this morning was about SYMMETRY, REFLECTIONS and INVERSES

LET'S START AND HAVE SOME FUN :)

When x is replaced with -x in the equation of a function y=f(x), its graph is reflected in y-axis.

*REFLECTION IN THE Y-AXIS ---- MAKE X-VALUES NEGATIVE*
*example*

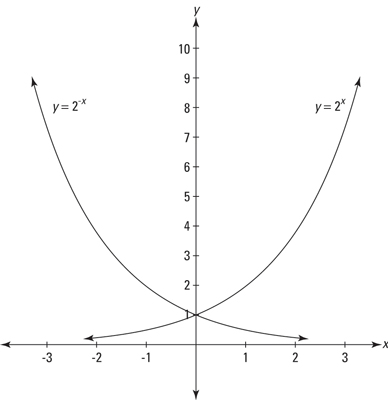
When y is replaced with -y in the equation of a function y=f(x), its graph is reflected in the x-axis.

* REFLECTION IN THE X-AXIS ---- MAKE Y-VALUES NEGATIVE*
*example*

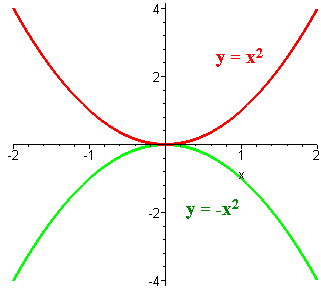
When x is interchanged with y in the equation of a function y=f(x), its reflected in the mirror line y=x. This is called INVERSE FUNCTION.

FINDING INVERSE EQUATION

1. Reflect f(x) with y.

2. Switch x and y.

3.Solve for y.

4. Replace y with inverse.

*REFLECTION IN THE MIRROR LINE ---- SWITCH X AND Y VALUES*
*example*

FUNCTION only touches the y value once.

---------SYMMETRY---------

EVEN FUNCTIONS are symmetric about the y axis. This means that negative and positive x-values result in the same y-values. It is symmetric between Quadrant I and II or quadrant III and IV. One example is a PARABOLA.

f(-x) ------ Means that x is negative and y is positive in Quadrant II.

f(x) ------- Means x and y are both positive in Quadrant I

OR

-f(-x) ----- Means that x and y are negative in Quadrant III

-f(x) ----- Means that xis positive and y is negative in Quadrant IV

ODD FUNCTIONS are symmetric about the origin. This means that positive and negative values result in different y-values. This happens between Quadrant I and III or Quadrant II and IV. An example of this is a VERTICAL CUBE.

f(-x) ----- Means that x is negative and y is positive in Quadrant II

-f(x) ----- Means that x is positive and y is negative in Quadrant IV

OR

f(x) ------ Means that x and y are both positive in Quadrant I

-f(-x) ---- Means that x and y are negative in Quadrant III

---------DETERMINING IF SHAPE IS A FUNCTION-----------

HORIZONTAL LINE TEST (HVT)

VERTICAL LINE TEST (VLT)

If horizontal line crosses through the graph only once and it has already passed the Vertical line test then the graph is ONE-TO-ONE FUNCTION.

IMPORTANT NOTE!!!!

---> Check VLT first and if it passes check HLT if it passes both it is a ONE-TO-ONE FUNCTION
---> If only the VLT is passed then it is a FUNCTION
---> If VLT fails don't check HLT and state NOT A FUNCTION

I HOPE EVERYONE LEARNED A LOT WITH MY POST!!! :)

SHEENA LOURANNE :)